The functioning of human body can be measured as a function of time by using different kinds of measurement systems. The time series acquired in these measurements are in general called biosignals. The most commonly studied biosignals include the electrocardiogram (ECG) and electroencephalogram (EEG) which are measurements of electrical activities of the heart and the brain, respectively. The analysis of biosignals is challenging, because extraction of useful information from these signals often necessitates complex mathematical models as well as knowledge of the underlying human physiology or neurophysiology.
Biosignal Analysis and Medical Imaging Group (BSAMIG) is lead by prof. Pasi A. Karjalainen. In addition, Adjunct prof. Mika Tarvainen is leading the team focusing on cardiovascular signal analysis and physiological modelling in BSAMIG.
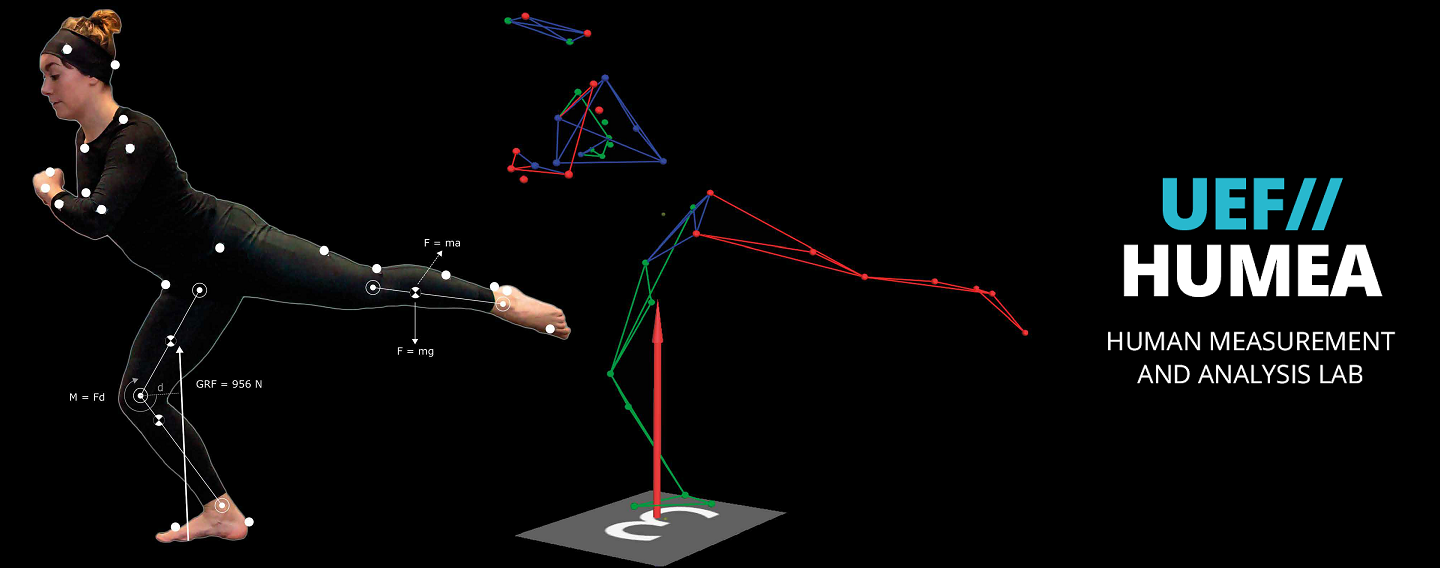
The main research topics of the group are currently human motion analysis, modelling of motor control in Parkinson’s disease, development of robot-assisted neurological rehabilitation methods, cardiovascular signal analysis methods, and psychophysiological measurements in assessing human behaviour and health. BSAMIG is maintaining HUMEA laboratory at Kuopio campus of the University. HUMEA laboratory has equipment and methods for human motion and performance analysis. Biosignal and motion measurements are utilized driving simulator environment of the laboratory and in developing robot-assisted neurological rehabilitation methods.
The research group is constantly involved in several regionally, nationally and internationally funded projects, and the collaboration with clinical and industrial partners is intensive.
Prof. Pasi Karjalainen (LinkedIn)
Pasi’s team:
Postdoc Researcher Paavo Vartiainen
Doctoral Researcher German Miroshnichenko
Doctoral Researcher Jere Lavikainen
Mika’s team:
Postdoc Researcher Jukka Lipponen
Doctoral Researcher Samu Sorola
Doctoral Researcher Saana Kupari
Active collaborators:
Professor Heikki Tikkanen, Institute of Biomedicine / Sports and Exercise Medicine
Adjunct Professor Hanna Pohjola
Adjunct Professor Lauri Stenroth
Doctoral Researcher Kim Lesch, Institute of Biomedicine / Sports and Exercise Medicine
Alumni:
Verneri Ruonala, PhD; Säteilyturvakeskus
Early Stage Researcher Dao T. A. Nguyen
Early Stage Researcher Lyydia Meuronen; IPG, UEF